Ballooning animals and Newtonian fitness (Ballonts III)

Click to enlarge; copyright Gert van Dijk

I have always had a weakness for balloon animals. Not the toy balloons that squeak when you twist them into shape, but lighter-than-air living beings. I would like to see such 'ballonts' float silently and majestically over the plains. One such is shown above (well, two of them). Nice, isn't it? I could do screensavers if anyone wants them.

Click to enlarge; copyright Gert van Dijk

Smaller ballonts, less than a meter, are even more to my taste. These might descend from a rain forest canopy to siphon fluids from carcasses, or something equally mysterious. No wind there, so it might be a good environment for them. They could flap around a bit as well.

Click to enlarge; copyright Gert van Dijk

Less dramatic but much more common would be tiny ballooning seeds drifting with the wind across the world, forming a sort of aerial plankton. Books on biomechanics never mention lighter-than-air flight, but do not discuss radial flight either, as neither exists on Earth. The usual question is whether the absence of lighter-than-air animals on Earth signifies that evolution so far forgot to take off in this direction or that the idea won't fly.

I have written about ballonts before (mostly here and here), but this time the focus will lie on 'hard science', so there will be some formulae and a few calculations. Sorry about that, but it is not really difficult. The goal is to see what is needed to achieve a ballont that can lift a nice hefty body with as small a gas bladder as possible. Because there is a bit of explaining to do we will not get further than Earth in this post.

The first step is to realise that floating in air works exactly the same as floating in water. As 'buoyancy' you will find that in biomechanics textbooks (for instance here and here). It all starts with Archimedes' principle, who stated that 'the upwards force of an object in water equals the weight of the displaced volume of water'. That works in air too, but let's start with water, because that is a bit more intuitive.

• Archimedes started with 'the displaced volume of water'. OK; let's make a box of 20 by 20 by 20 cm and hold it under water. It is not difficult to find the volume of the water it displaces: that is the volume of the box itself, which is 0.2 x 0.2 x 0.2 = 0.008 cubic meters.
• To get weight we first need to know what the mass of that amount of water is. The density of fresh water is 1000 kg per cubic meter (sea water is a bit denser). For 0.008 cubic meter, we get a mass of 0.008x1000= 8 kg.
• Weight is a force, not a mass. It is the product of mass with the gravity constant g, and on earth that is 9.8 m/(s^2). So the upwards force acting on our box is 9.8x8= 78.4 Newton.

Upward force = g x Density of water x Volume of object

Nice, but so what? Well, the presence of g in the formula means that the upward force increases directly with gravity. On a world with twice the gravity of Earth the upwards force will be twice as large as on Earth. One consequence of this is that a floating object rises faster than on Earth. But will it also lift a larger body mass, which is what we want? As we will see, the answer is no, but first we have to calculate how much mass a balloon can lift. The first step to get there is to calculate the object's own weight. We know how to calculate weight: upwards force was weight of water, after all:

object weight = g x Density of object x Volume of object

The net force is obtained by subtracting them, which can be written as follows:

net force= g x (Density of water - Density of object) x Volume of object

The gravity constant g is still in there, but focus on the rest of the formula. If the object is denser than water the net force is downwards -it sinks- and if the object is less dense, it will float. No matter what you do to g, that balance will not change. Interesting; the amount of mass that can be lifted does not depend on gravity. Without g, the formula describes a mass (density times volume). For a net upwards force, that resulting mass is what the object can lift:

liftable mass= (Density of water - Density of object) x Volume of object

Here is an example: Suppose the object is made of cork with a density of 250 kg/cubic meter. Fill in the numbers for cork and fresh water and you get (1000-250) x 0.0008 = 6 kg. If you tie a mass of 6 kg from the cork cube, the ensemble would just stay in place under water, as its combined density now is the same as that of water. (1) All we need to do to turn this into a formula for the bladder of a ballont in air is to supplant 'water' with 'air', and 'object' with 'bladder':

liftable mass= (Density of air - Density of bladder) x Volume of bladder

The density of air on earth at sea level is only about 1.2 kg per cubic meter, so we need very light materials to make a ballont work. The choices are limited. Helium would be great, but it is probably difficult to find on a terrestrial planet, and concocting a biochemistry to produce helium may be taking things too far. Hydrogen is easy to find, can be fabricated, and only weighs 0.09 kg per cubic meter. We are now almost ready for the real stuff.

Click to enlarge; copyright Gert van Dijk

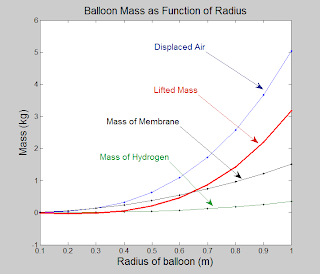
The image above shows a simple ballont scheme. It builds on the scheme above. Here are the ingredients, supposed to work at one Earth atmosphere and 20 degrees centigrade:

• A spherical bladder. It consists of a membrane, which will weigh something. I have great faith in the ability of Darwinian evolution to come up with amazing substances, so I chose something like Mylar. The membrane will be just 0.1 mm thick, and its density is 1.2 times that of water, based on PET and similar substances. The radius of the sphere allows its area to be calculated, and with that its mass. That is a downwards force.
• The bladder contains hydrogen gas. Its radius gives us its volume, and together with the density of hydrogen (0.084 kg/(m^3) at about 20 degrees) we get the mass of the hydrogen. This is another downwards force.
• The volume of the displaced air is found from the radius of the bladder and the density of air (1.2 kg/(m^3)). This is an upwards effect.

Subtract the two downwards effects from the one upwards one. What we have left is how much mass the bladder can lift. We will tie a body underneath with a density of 1.1 times that of water. (2)

Click to enlarge; Copyright Gert van Dijk

Click to enlarge; copyright Gert van Dijk

The graph above shows results for bladders of 0.1 to 1 meter radius. The blur line (displaced air) is what determines the upwards force, and the membrane (black) and the hydrogen (green) pull downward. The red line is the difference, and that determines the mass of a body you can suspend from the bladder. Hm; a balloon with a radius of one meter still only lifts about 3 kg, as shown in the image below the graph (the man is a 3D object I found on the internet). While 3 kg is enough to build an interesting animal -think of a cat!- the relative sizes of the bladder and the body mass are not pleasing. Even if we clap on some wings to the body, the animal will still be extremely vulnerable to the slightest wind. It does not even get close to the kind of animal we want. I think we need to do better. Even a protoballont should have some advantage of its bladder, or else Darwinian evolution will not take off.

Click to enlarge; copyright Gert van Dijk

Perhaps the ballont seedlings work better, so let's do the job for a radius of up to 40 cm. Hang on: the red line goes below zero, so the smaller ones cannot lift anything at all! The reason is that their membrane is too heavy at small sizes. On further reflection that is understandable: the mass of the membrane increases with the square of the radius, and lifting ability (volume) with the third power. For very small ballonts, the membrane can outweigh the lifting power! Alas, there go the balloon seedlings. Struck down, not by a lack of Darwinian fitness, but because they are unfit in a Newtonian universe.

Click to enlarge; copyright Gert van Dijk

Let's try again for balloons with a radius of 1 to 5 meter. That's better: we can lift hundreds of kg now, enough for an impressive animal, with limbs, a digestive system, a hydrogen-producing organ (however that works), tentacles for tethering and grasping food, etc.. You may protest that the membrane is too flimsy for an animal of this size. I agree, but even with a thicker membrane, compartments etc., the effect of the third power of volume will easily priduce a net lifting force. Unfortunately, a balloon with a 5 meter radius is still very large indeed, nowhere near the shape we were looking for....

So it is the density difference of the lifting gas compared to the surrounding air that makes a balloon work. Perhaps surprisingly, gravity does not determine the liftable mass, or, at any rate, not directly. Some elements scale with the square of the radius and others with the third power. We saw earlier that this limits the size of land animals (start here for that subject). For ballonts it is just the opposite: bigger is better, at least as far as liftable mass is concerned. Whether the animal is viable in the Darwinian sense is something else entirely. Earth is a poor place for ballonts: blame Newton. To get them to work we need to manipulate not the ballont, but the planet! More on that in the future.

(1) In reality, the object you tie underneath the object also has both weight and an upwards force. The figure of 6 kg holds for the mass difference between the two.
(2) The body also displaces a bit of air, but that has so little mass we will ignore its upwards force.